“I pianeti si muovono su orbite ellittiche in cui il Sole occupa uno dei due fuochi”.
E’ con questa semplicissima frase che agli inizi del diciassettesimo secolo l’astronomo tedesco Giovanni Keplero s’impose nella comunità scientifica, distruggendo il cosiddetto sistema geocentrico tolemaico e confermando le ipotesi copernicane di centralità del Sole.
Sebbene tutto sembri rivoluzionario in quella che passerà alla storia come “Prima legge di Keplero”, esiste al suo interno un termine che più di tutti dovrebbe lasciarci con il fiato sospeso.
Ellittiche.
Orbite ellittiche.
Prima di chiederci perché questo termine sia così sconvolgente, assicuriamoci di parlare la stessa lingua.
Secondo la geometria classica l’ellisse è il luogo geometrico (insieme) di punti tali per cui la somma della loro distanza dai due fuochi è costante.
Alla luce di questo si evince quanto sia forte il legame che tiene strette tutte le entità unidimensionali di questa figura.
E per sincerarci della perfezione che lega i suddetti elementi, scomodiamo la geometria analitica che ci fornisce un’espressione chiara e semplice dell’equazione di un’ellisse:
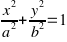
Alla luce di quanto abbiamo appena scoperto la domanda sembra quasi sorgere spontanea: come è possibile che il fenomeno che descrive il comportamento meccanico del nostro intero Sistema Planetario sia descritto da una così semplice equazione?
Pianeti, giganti rocciosi e gassosi che viaggiano indisturbati seguendo una traiettoria descritta in maniera quasi elementare.
Queste considerazioni non possono che portare alla luce domande sulla struttura intrinseca dell’universo stesso. Le equazioni di cui parliamo -che sono alla base del nostro sistema di calcolo- si ripropongono senza la minima variazione nello spazio profondo creando un indissolubile legame tra quello che c’è qui e tutto quello che troviamo lì fuori.
E’ difficile in questi termini non pensare ad un ordine cosmico e perché no, anche ad un intervento che trascenda le semplici leggi del caso (e del caos).
Ma prima che le nostre menti si perdano in ragionamenti metafisici c’è ancora un’estensione che manca al nostro discorso. I pianeti non sono infatti gli unici a muoversi lungo queste particolari curve.
Nell’ambito della meccanica del volo spaziale –branca che studia il moto di satelliti e navicelle nello spazio- è facilmente dimostrabile che l’equazione delle traiettorie di tali oggetti è la seguente:
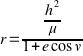
Tralasciando il significato dei simboli che compaiono (di cui si riportano i nomi a fine articolo), ciò che sorprende è che nuovamente, tale traiettoria risulta essere quella di una conica che definisce diverse figure geometriche nello spazio quali ellisse, iperbole, parabola.
Insomma, tutto gira intorno al Sole e ai corpi attrattori seguendo le leggi di gravità, e se Keplero ha saputo inserirsi nella storia con le sue rivoluzionarie scoperte, la matematica ne ha legittimato l’eternità.
h= momento angolare.
μ= parametro gravitazionale.
e= eccentricità dell’orbita.
ν=anomalia vera.








